Difference between revisions of "Kerr - June 30, 2016"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
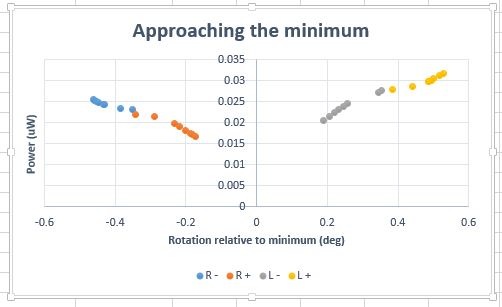
[[file:LRappmin.jpeg|thumb|upright=2|In this graph the measured powers at the left and right of the minimum are in relation to a arbitrary rotation with 0 being perfect perpindicular interception of the polarizers.]] | [[file:LRappmin.jpeg|thumb|upright=2|In this graph the measured powers at the left and right of the minimum are in relation to a arbitrary rotation with 0 being perfect perpindicular interception of the polarizers.]] | ||
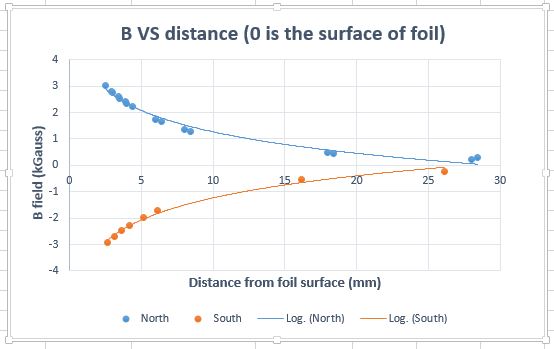
| − | [[file:Bvsdistance.jpeg|thumb|upright=2|This relationship will be important down the road for further Kerr effect calculations. The fit at this time is not completely accurate, I plan to touch it up when a presentation is closer or when I have some down time. ]] | + | [[file:Bvsdistance.jpeg|thumb|upright=2|This relationship will be important down the road for further Kerr effect calculations. The fit at this time is not completely accurate, I plan to touch it up when a presentation is closer or when I have some down time.]] |
| + | I also graphed a normalized version of minimum approaching data set. However, I am concerned that both of these shapes are not able to fit to our standard Δ p = A*sin<sup>2</sup> θ | ||
| + | |||
| + | After a few attempts to fit with excel, I was unsuccessful. I may have to utilize Extrema or Canopy with Python. | ||
Revision as of 21:39, 30 June 2016
I also graphed a normalized version of minimum approaching data set. However, I am concerned that both of these shapes are not able to fit to our standard Δ p = A*sin2 θ
After a few attempts to fit with excel, I was unsuccessful. I may have to utilize Extrema or Canopy with Python.