Kerr - June 30, 2016

In this graph the measured powers at the left and right of the minimum are in relation to a arbitrary rotation with 0 being perfect perpindicular interception of the polarizers.

This relationship will be important down the road for further Kerr effect calculations. The fit at this time is not completely accurate, I plan to touch it up when a presentation is closer or when I have some down time.

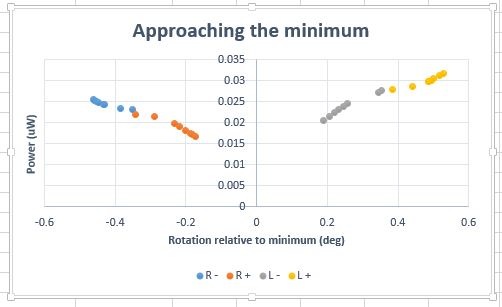
I also graphed a normalized version of minimum approaching data set. However, I am concerned that both of these shapes are not able to fit to our standard Δ p = A*sin² θ

After a few attempts to fit with excel, I was unsuccessful. I accomplished some fits but I believe they could be better. I may have to utilize Extrema or Canopy with Python.

Check it out here -->> media:LRappminfit.xlsx

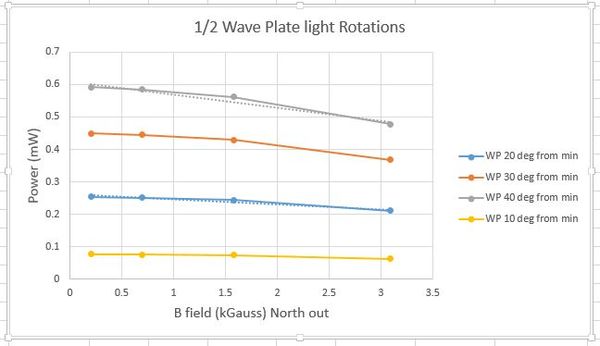
In order to further solidify our Kerr effect claims, Joe came up with an experiment utilizing the half-waveplate. Since we should be dealing with a sin² graph, we should see different slopes at different starting points of power. I rotated the half-Waveplate (mind you it is twice that reported) 10, 20, 30, and 40 degrees which corresponds to 20, 40, 60, and 80 degrees of rotation on the vertically polarized light.

We do in fact see different slopes for all 4 different starting points.

Check out the work here --> media:multislopeexpgraphs.xlsx